微分ゼミ 3回目 (2017.10.26)

1 微分とは

1.1 前回の質問

下記のような質問がありました。

\(dx\)って何ですか？
偏微分って何ですか？
平均値の定理は，何を意味していて，何故重要なのですか？
全微分は何を求めているのですか？
- 全微分は，全変化量のこと。
  - y=f(x) => d(y) = d(f(x)) = lim f(x+dx)-f(x) = f'(x) dx
  - z = f(x,y) => d(z) = d(f(x,y)) dz = lim f(x+dx, y+dy) - f(x,y) = lim f(x+dx, y+dy) - f(x+dx, y)
    - lim f(x+dx, y) - f(x, y)

曲線 \(f_1\) の求め方は？

自分は理解できているか，確認してみてください。

先生の答えや考えは，今日のプリントの中に書かれているはずです。

1.2 前回のまとめのまとめ

今回は，ベクトルを使って微分の本質を説明してみます。

以下，\(\vec{e_x}\), \(\vec{e_y}\), \(\vec{e_z}\) は \(x\)と\(y\)と \(z\)方向の単位ベクトルとします。

\(\Delta x\), \(\Delta y\), \(\Delta z\) は \(x\)と\(y\)と\(z\)方向の変化量とします。

\(dx\)，\(dy\)， \(dz\) は，\(dx = \lim_{\Delta x \rightarrow 0} \Delta x \), \(dy = \lim_{\Delta y\rightarrow 0} \Delta y \), \(dz = \lim_{\Delta z \rightarrow 0} \Delta z \) で定められる0に近づいていく微小変化量を表わします。

\(dx\)，\(dy\)， \(dz\) は，それだけで考えると，ゼロとみなせる微小量ですが，\(y=f(x)\) や \(z=f(x,y)\) などの関係があると， \(dy\) と\(dx\)，\(dz\) と \(dx\) と\(dy\) の間にも成り立つ関係式があり，それが微分係数だったり，導関数だったり，全微分の式だったりします。

1.2.1 関数の変化と微分 (1変数関数)

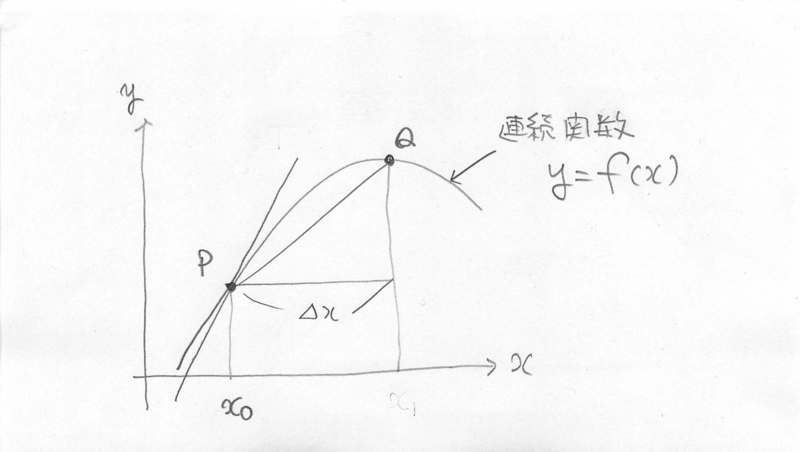
ベクトル \(\vec{PQ}\) を考えます。 \(\vec{PQ}\) は下記のように表わせます: \begin{eqnarray} \vec{PQ} &=& \Delta x \vec{e_x} + \Delta y \vec{e_y} \\ & = & \Delta x\, \vec{e_x} + ({f(x_0+\Delta x) - f(x_0)}) \vec{e_y} \\ & = & \Delta x\, \vec{e_x} + \left(\frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}\right){\Delta x} \vec{e_y} \end{eqnarray}
途中，変化量(\(f(x_0+\Delta x) - f(x_0)\)) を
平均変化率 (\(\frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}\)) と変位\((\Delta x)\) の積で表わしています。
\(P\rightarrow Q\) の極限を考えると以下になります: \begin{eqnarray} \lim_{Q \rightarrow P} \vec{PQ} & = & \lim_{\Delta x \rightarrow 0} \left(\Delta x \vec{e_x} + \Delta y \vec{e_y}\right) \\ & = & \lim_{\Delta x \rightarrow 0}\left(\Delta_x \vec{e_x} + (f(x_0+\Delta x) - f(x_0))\vec{e_y} \right)\\ & = & \lim_{\Delta x \rightarrow 0}\left(\Delta_x \vec{e_x} + \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} {\Delta x}\,\vec{e_y} \right)\\ & = & dx \, \vec{e_x} + f'(x) dx \vec{e_y}\\ & = & dx \, \vec{e_x} + dy \vec{e_y}\\ \end{eqnarray}
\(\lim_{Q\rightarrow P}\vec{PQ}\) の \(\vec{e_y}\)成分に注目すると \( dy = f'(x_0) dx \) が導かれます。
つまり，\( dx \) も \( dy \) も 0 に近づいていきますが， \(y = f(x) \)という関係があるため，点P\((x_0，y_0)\)において，\( dy \) は \( dx \) に比べて， \(f'(x_0)\) 倍で 0 に近づいていくことになります。

1.2.2 2変数関数の変化と微分

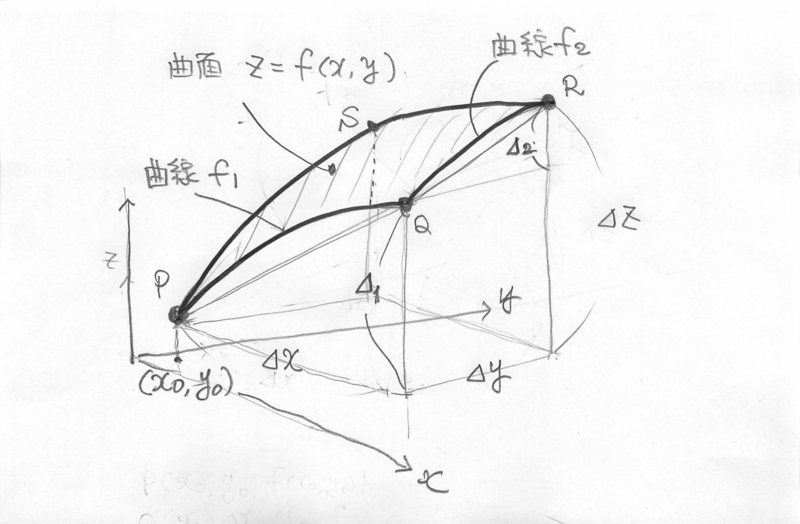
曲線 \(f_1\)の変化量 \(\Delta_{1}\)，曲線 \(f_2\)の変化量\(\Delta_{2}\) を表わす式。
- \(\Delta_{1} = f(x_0+\Delta{x},y_0) - f(x_0,y_0) \)
- \(\Delta_{2} = f(x_0+\Delta{x},y_0+\Delta{y}) - f(x_0+\Delta{x},y_0) \)
極限を取ると偏微分係数になります:
- \(\lim_{\stackrel{\Delta{x} \rightarrow 0}{\Delta{y} \rightarrow 0}} \Delta{1} = f_x(x_0,y_0)dx \)
- \(\lim_{\stackrel{\Delta{x} \rightarrow 0}{\Delta{y} \rightarrow 0}} \Delta{2} = f_y(x_0,y_0)dy \)

ベクトル \(\vec{PR}\) を考えます。
\(z = f(x, y)\) という関係があるので， \(x\) と \(y\) は独立に動けますが，\(z=z(x,y)\)です。

\(\vec{PR}\) は下記のように表わせます:

\begin{eqnarray} \lim_{R \rightarrow P }{\vec{PR}} &=& dx\vec{e_x} + dy\vec{e_y} + dz\vec{e_z} \\ & = & dx \vec{e_x} + dy \vec{e_y} + (f_x(x_0, y_0) dx+ f_y(x_0, y_0){dy})\vec{e_z} \\ & = & (dx \vec{e_x} + f_x(x_0, y_0) dx \vec{e_z}) \\ & & + (dy \vec{e_y} + f_y(x_0, y_0)dy) \,\vec{e_z} \end{eqnarray}

2 平均値の定理からテイラーの定理へ

2.1 平均値の定理の意味

\([a, b]\) で微分可能な関数 \(f(x)\) に対する，平均値の定理は次のように解釈できると考えます。

読んで自分で考え，納得できれば自分の言葉でまとめてください.

区間 \([a,b]\) の間に，接線の傾きが平均変化率となる点 c が存在する。

\begin{eqnarray} f(b) - f(a) & = & f'(c)\,(b-a), & a< c < b \\ \end{eqnarray}

上式の\(b\rightarrow a\)の極限が，\(dy=f'(x)dx\)となる。
両辺を \((b-a)\)で割り，\(b\rightarrow a\)の極限が，\(dy/dx = f'(x) \)となる。
\(f(a)\)の値から，\(f(b)\)の値を正確に計算できる。

\begin{eqnarray} f(b) &=& f(a) + f'(c) \, (b-a), a < c < b \\ \end{eqnarray}

但し，\(c\)の値がわからないと\(f(b)\)の値は正確に求められないが，

近似を用いながら，だんだんに \(f(b)\)を求めていくことができる。 \(\sqrt{10}\)の計算や次節のやり方などがその例。

2.2 平均値の定理を繰り返す

\(h = b -a\) とし，\(c\) の代わりに，\(c = a + \theta_1 h\) と書き変え，平均値の定理を下記のように書く。繰り返すごとに新しい\(\theta\) がでてくるので，添字を付ける。

\begin{eqnarray} f(a+h) &=& f(a) + f'(a+\theta_1 h) h, & 0 < \theta_1 < 1 \\ & & & h=(b-a) \end{eqnarray}

上式を，\(a\) から \(h\) だけ離れた \(b\) での \(f(b) \) を求める式と考える。
\(f(x)\) の導関数と，\(f(a)\) と， \(f'(a+\theta_1 h)\) が分れば，\(f(b)\) が求められる。
しかし，\(\theta_1\)が分らないため，\(f'(a+\theta_1 h)\) が求められない。

そこで，\(f'(a+\theta_1 h)\)に，平均値の定理を適用し，\(f'(a)\)を使って，表してみよう。

次の式 (の\(\cdots\)の部分) を自分で導いてみてください。

\begin{eqnarray} f'(a+\theta_1 h) & = & f'(a) + \cdots \end{eqnarray}

\(f^{(2)}(a+\theta_1\theta_2 h)\) についても，平均値の定理を適用し， \(f^{(2)}(a)\)を使って，計算式を導いてみよう。

\(f^{(n)}(a+\theta_1\theta_2\cdots\theta_{n} h)\) についても，平均値の定理を適用し， \(f^{(n)}(a)\)を使って，計算式を導いてみよう。

結局，\(f(b)\) の計算式はどうなる？

テイラーの定理みたいのが導けましたか？